-
빅데이터분석기사 실기 준비 - Day 6자격증/빅데이터분석기사 2021. 12. 2. 02:34728x90반응형
8. 투표기반 앙상블(voting)
- 투표기반 앙상블은 여러 분류기를 학습시킨 후 각각의 분류기가 예측하는 레이블 범주가 가장 많이 나오는 범주를 예측하는 방법
- 다수결 원리
- 개별 분류기의 최적 하이퍼파라미터를 찾은 후, 투표기반 앙상블로 모델을 만들어 좀 더 좋은 분류와 회귀 예측을 찾는 것
- 아래 그림은 여기서 가져옴
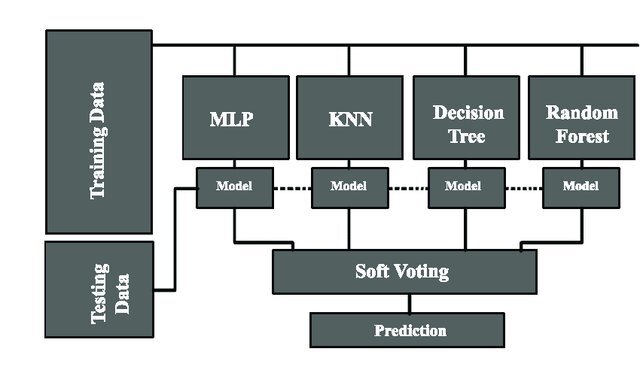
- (분류 알고리즘의 경우) 투표기반 앙상블의 옵션
- 범주 기반: Hard Learner
- 확률 기반: Soft Learner
- ensemble => VotingClassifier, VotingRegressor
<VotingClassifier: Hard>
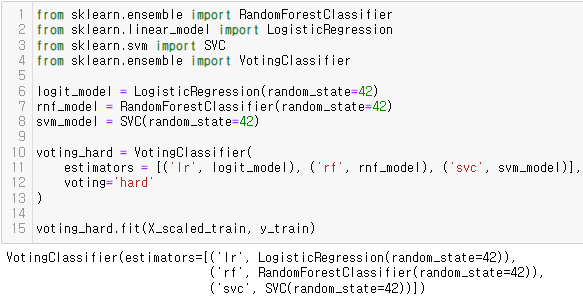
<VotingClassifier: Soft>

- 범주(Hard)보다 확률(Soft) 방식이 다소 정확도가 높음
<VotingRegressor>

9. 앙상블 배깅(baggin)
- 학습 데이터에 대해 여러 개의 부트스트랩(bootstrap) 데이터를 생성하고 각 부트스트랩 데이터에 하나 혹은 여러 알고리즘을 학습시킨 후 산출된 결과 중 투표(Voting) 방식에 의해 최종 결과를 선정하는 알고리즘

https://towardsdatascience.com/ensemble-learning-bagging-boosting-3098079e5422 - ensemble => BaggingClassifier, BaggingRegressor
- 주요 하이퍼파라미터
- n_estimators : 부트스트랩 데이터셋 수
<BaggingClassifier>
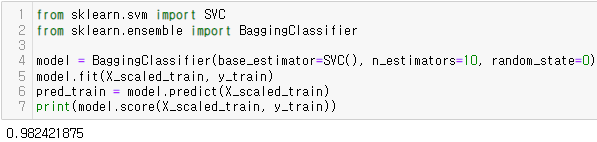
<BaggingRegressor>

10. 앙상블 부스팅(Boosting)
- 부스팅은 여러 개의 약한 학습기(weak learner)를 순차적으로 학습시켜 예측하면서 잘 못 예측한 데이터에 가중치를 부여하여 오류를 개선해 나가며 학습하는 앙상블 모델임
- 배깅이 한 번에 여러 개의 데이터셋에서 학습한 결과를 종합하는 병렬식 앙상블인 반면, 부스팅은 앞에서 학습한 모델 결과를 바탕으로 두 번째 모델에서 오류를 수정하고 세 번째 모델에서 또 오류에 중점을 두어 해결해 나가는 순차적인 직렬식 앙상블
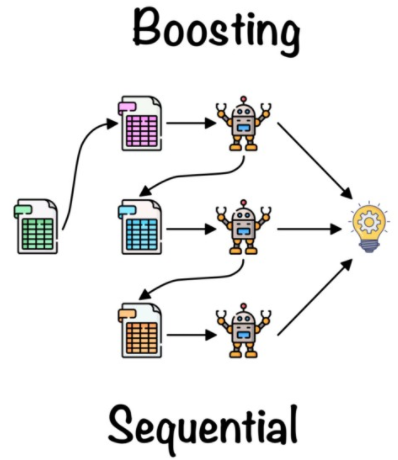
https://towardsdatascience.com/ensemble-learning-bagging-boosting-3098079e5422 - ensemble => AdaBoosting(AdaBoostClassifier, AdaBoostRegressor), GradientBoosting(GradientBoostingClassifier, GradientBoostingRegressor)
- AdaBoosting 주요 하이퍼파라미터
- base_estimator
- n_estimators
- GradientBoosting 주요 하이퍼파라미터
- learning_rate
- n_estimators
11. 앙상블 스태킹(Stacking)
- 스태킹은 데이터셋이 아니라 여러 학습기에서 예측한 예측값(predict value)으로 다시 학습 데이터를 만들어 일반화된 최종 모델을 구성하는 방법
- 핵심적 차이는 데이터셋이 아닌 예측값들로 예측을 한다는 idea

https://stats.stackexchange.com/questions/350897/stacking-without-splitting-data - ensemble => StackingClassifier, StackingRegressor
- 주요 하이퍼파라미터
- estimators
<StackingClassifier>

<StackingRegressor>

12. 선형 회귀모델
- 연속형 원인변수가 연속형 결과변수에 영향을 미치는지를 분석하여 변수를 예측하기 위한 목적으로 사용됨
- x가 a만큼 증가하면 y가 얼마나 증가하는지 기울기(β1)를 구하고 x가 0일 때 y의 기본값인 상수항 β0(y 절편)을 구해 y=β0+β1x 와 같은 1차식을 도출함
- 아래는 단일 회귀분석이고 다중 최귀분석도 있음

https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80 - 설명력 R^2: 실제값과 예측값 간에 얼마나 일치하는지 or 차이나는지를 계산
- linear_model => LinearRegression
or
statsmodel.api => OLS(y_train, X_train) 사용
<Statsmodels 사용>
- add_constant를 통해 상수항 변수를 추가함

- 모델 생성과 훈련

- results.summary 결과

R-squared : 설명력
coef : x변수가 1증가할 때 y가 변화하는 정도, 기울기
p<|t| : 통계적으로 유의한가
13. 릿지(Ridge) 회귀모델
- 릿지 회귀모델은 선형회귀분석의 기본원리를 따르나 가중치(회귀계수) 값을 최대한 작게 만들어, 즉 0에 가깝게 만들어 모든 독립변수(특성)가 종속변수(레이블)에 미치는 영향을 최소화하는 제약(regularization)을 반영한 모델임
- 선형관계뿐만 아니라 다항곡선 추정도 가능
- 주요 하이퍼파라미터
- alpha : 값이 클수록 규제가 강하며 회귀계수가 0에 근점함 반면 0에 가까울수록 규제를 하지 않아 선형회귀와 유사한 결과를 보임
- linear_model => Ridge
14. 라쏘(Lasso) 회귀모델
- 라쏘 회귀모델은 릿지 회귀모델과 유사하게 특성의 계수값을 0에 가깝게 하지만 실제 중요하지 않은 변수의 계수를 0으로 만들어 불필요한 변수를 제거하는 모델임
- linear_model => Lasso
- 주요 하이퍼파라미터
- alpha : 커지면 계수를 0에 가깝게 제약해 훈련데이터의 정확도는 낮아지지만 일반화에서는 기여. 반면 alpha가 0에 가까울수록 회귀계수를 아무런 제약을 하지 않은 선형회귀와 유사하게 적용
15. 엘라스틱넷
- 릿지회귀와 라쏘회귀를 절충한 모델
- 규제항은 릿지와 라쏘의 규제항을 단순히 더해서 사용
- r을 조절하여 사용하는데 r=0이면 릿지와 같고 r=1이면 라쏘와 같음

- linear_model => ElasticNet
- 주요 하이퍼파라미터
- alpha : 커지면 계수를 0에 가깝게 제약해 훈련데이터의 정확도는 낮아지지만 일반화에서는 기여. 반면 alpha가 0에 가까울수록 회귀계수를 아무런 제약을 하지 않은 선형회귀와 유사하게 적용
16. 군집분석(cluster analysis)
- 개체들의 특성을 대표하는 몇 개의 변수들을 기준으로 몇 개의 그룹으로 세분화하는 방법
- 개체들은 다양한 변수를 기준으로 다차원 공간에서 유사한 특성을 가진 개체로 묶음
- 개체들 간의 유사성은 개체 간의 거리를 사용하고 거리라 상대적으로 가까운 개체들은 동일 군집으로 묶음
- 개체 간의 거리를 행렬을 이용해 계산함(대표적으로 유클리디안 거리(그냥 거리 공식) 계산)
- cluster => Clustering
- KMeans
- 주요 하이퍼파라미터
- n_clusters : 몇 개의 군집으로 묶을 것인가를 결정
<KMeans>
- 데이터 불러오기

- 아래는 통계 기준으로 최적의 군집 수를 찾기 위한 과정
- 핵심은 군집수를 1~21개까지 늘려보면서 'kmeans.inertia_' 값을 살펴보는 것
- 'kmeans.inertia_'는 군집의 중심과 각 케이스(개체) 간의 거리를 계산함
- 중심과 개체간의 거리가 작아진다는 것은 그만큼 군집이 잘 형성이 되었다는 것임

- 크게 감소하다가 변화가 없는 지점에서 최적의 군집 수 k를 결정
- 5로 결정!
- X에 대해 훈련된 kmeans를 예측하여 y_kmeans 얻음
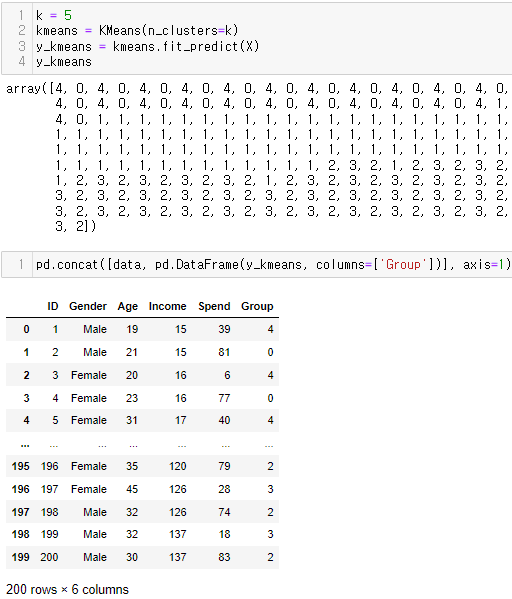
- 5개 군집의 중심좌표 확인하기

- 학습(fit)만 한 후 결과들을 kmeans_pred에 담음
- 그 중 '.cluster_centers_'가 각 좌표의 중심점 결과가 담겨진 객체임
- 다음은 군집 예측하기

- 군집 이름 만듦
- 산점도 그리기
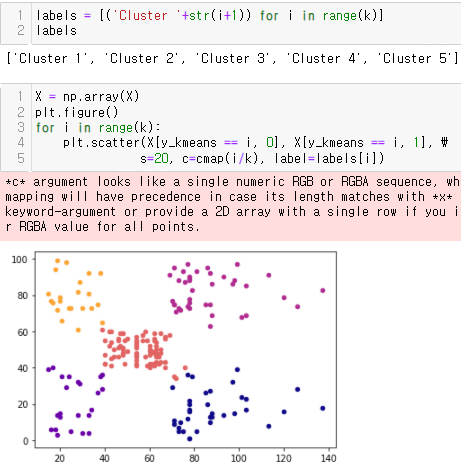
- 군집의 중심점만 찍기


- 군집분석 계산과정 살펴보기
- 데이터 불러오기

- 기술통계를 살펴보면 4가지 변수의 단위가 다름 => 정규화 과정 필요

- 정규화 적용

- 중심점을 centroids에 담음
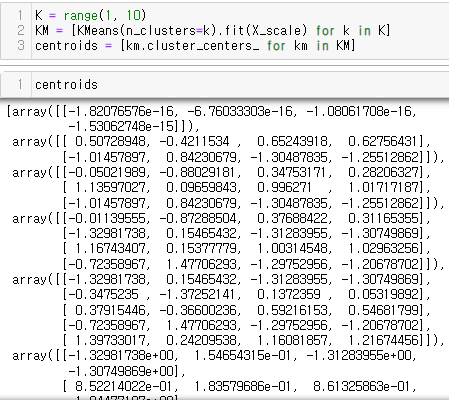
- cdist 거리계산 라이브러리를 이용해 유클리디안 방법으로 거리 계산함

- 계산한 거리 중 최솟값(np.argmin)을 cIdx에 담음
- dist로 최솟값을 구함
- avgWithinSS: 군집의 중심과 개체들 간의 최소 거리들의 평균을 구해 저장한 값


- 각 군집 내에 wcss는 개체들간의 거리를 제곱하여 더한 값임
- tss는 전체 개체들 간의 거리들을 제곱하여 개체수로 나눈 것
- bss는 둘 차이

p318~321 패스
<Hierarchical clustering>
- kmeans는 비계층적 방법이며 분석속도가 빠르고 군집을 형성하면서 유연하게 다른 군집으로 다시 재군집화가 가능한 반면, 계층적 군집분석은 한 번 어떤 군집에 속한 개체는 분석과정에서 다른 군집과 더 가깝게 계산되어도 다른 군집화가 허용되지 않는 방법임
- 속도도 다소 오래 걸림
- 계층적 군집에서 개체들 간에 군집이 형성되는 과정을 파악하기 위해 sch 사용
- 개체들 간의 거리를 ward 방법으로 하고 dendrogram을 그림

- 군집수를 5로 하여 병합군집(AgglomerativeClustering)을 적용한 군집분석 수행
- 이 방법은 시작할 때 각 포인트를 하나의 클러스터로 지정하고 그 다음 종료 조건(지정한 군집 수)을 만족할 때까지 가장 비슷한 두 클러스터를 합치는 방식으로 진행하는 군집분석임

- 군집분석 시각화

17. DBSCAN
- DBSCAN은 밀도기반 클러스터링 기법임
- 케이스가 집중되어 있는 밀도(density)에 초점을 두어 밀도가 높은 그룹을 클러스터링 하는 방식
- 중심점을 기준으로 특정한 반경 이내에 케이스가 n개 이상 있을 경우 하나의 군집을 형성하는 알고리즘

https://www.kdnuggets.com/2020/04/dbscan-clustering-algorithm-machine-learning.html - 주요 하이퍼파라미터
- eps(epsilon) : 근접 이웃점을 찾기 위해 정의 내려야 하는 반경 거리
- min_samples(minPts) : 하나의 군집을 형성하기 위해 필요한 최소 케이스 수
- 데이터의 케이스(포인트)는 3가지로 분류함
- Core point : epsilon 반경 내에 최소점(minPts) 이상을 갖는 점
- Border point : Core point의 epsilon 반경 내에 있으나, 그 자체로는 최소점(minPts)을 갖지 못하는 점
- Noise point : Core point도 아니고 Border point도 아닌 점
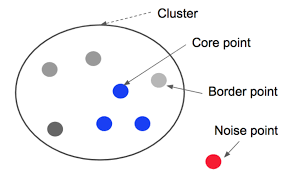

https://www.researchgate.net/figure/DBSCAN-core-border-and-noise-points_fig1_258442676 - cluster => DBSCAN
<DBSCAN>
- DBSCAN 모델 생성

- dbscan 모델에 iris_data를 학습(fit) 시킨 후, dbscan.labels_를 확인
- 위에서 설정한 기준에 따라 2개의 군집(0, 1)로 나타났고 모델 기준에서 이상치는 -1로 표현됨

- 학습시킨 결과를 pred에 할당

[시각화]
- 군집화 경향과 이상치를 도표에 표현
- 변수가 4개이므로 4차원의 공간에 데이터가 위치하는데 우리는 4차원 표현 불가
- 그러므로 decomposition의 차원축소 방법인 '주성분 분석(PCA)'를 가져옴

- 시각화

18. 연관규칙분석
- 연관규칙은 Apriori Algorithm이라고 하며 대용량의 트랜잭션 데이터(거래 데이터)로부터 'X이면 Y이다'라는 형식의 연관관계를 발견하는 기법임
- 어떤 두 아이템 집합이 빈번히 발생하는가를 알려주는 일련의 규칙들을 생성하는 알고리즘
- 흔히 장바구니 분석이라고 함
- 소비자들의 구매 이력 데이터를 토대로 'X 아이템을 구매하는 고객들을 Y 아이템 역시 구매할 가능성이 높다'는 행동을 예측 또는 추천하게 됨
- 연관규칙을 수행하기 위해서는 거래데이터(transaction data)의 형식으로 되어 있어야 함
- 이러한 데이터를 바탕으로 연관규칙은 지지도(support), 신뢰도(confidence), 향상도(lift)를 구하고 두 개 이상의 동시 구매 발생의 규칙을 계산한 지표를 바탕으로 도출해 냄
- 지지도: 전체 거래 건 수 중에서 X와 Y를 모두 포함하는 거래 건수의 비율 => n(X∩Y)/N(전체)
- 신뢰도: X를 포함하는 거래 중에서 Y도 포함하는 거래 비율 => n(X∩Y)/n(X)
- 향상도: X가 주어지지 않았을 때의 Y의 확률 대비 X가 주어졌을 때 Y의 확률 증가 비율. 신뢰도/P(Y)
향상도가 절대값 1보다 크면 우수함을 의미. 1이면 X와 Y는 독립적임
연관규칙의 신뢰도/지지도 = c(X->Y)/s(Y)
- from apyori import apriori
- 주요 하이퍼파라미터
- min_support : 최소 지지도
- min_confidence : 최소 신뢰도
- min_lift : 최소 향상도
<apyori -> apriori>
- !pip install apriori
- transaction data로 변환

- 연관규칙 적용

- 판다스로 확인
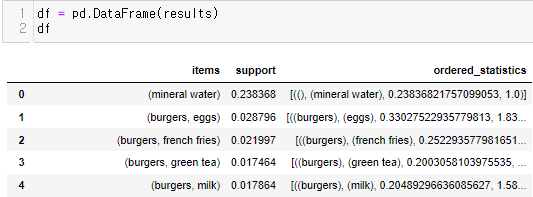
- 74개 뽑음
 728x90반응형
728x90반응형'자격증 > 빅데이터분석기사' 카테고리의 다른 글
빅데이터분석기사 실기 준비 - Day 5 (2) (0) 2021.12.01 빅데이터분석기사 실기 준비 - Day 5 (1) (0) 2021.11.30 빅데이터분석기사 실기 준비 - Day 4 (0) 2021.11.30 빅데이터분석기사 실기 준비 - Day 3 (0) 2021.11.26 빅데이터분석기사 실기 준비 - Day 2 (0) 2021.11.25