-
[Data Structure] DFS vs BFS with PythonData Structure 2022. 2. 23. 00:41728x90반응형
아래 글을 보고 공부한 후 정리, 번역한 글입니다.
Reference
https://medium.com/nothingaholic/depth-first-search-vs-breadth-first-search-in-python-81521caa8f44
Depth-First Search vs. Breadth-First Search in Python
The simplified explanation of the two traversals algorithm.
medium.com
1. Tree traversal
- 트리 순회는 노드를 반복하지 않고 정확히 한 번 각 노드를 checking(visiting)하거나 업데이트하는 것으로 알려져 있음
- 모든 노드는 간선을 통해 연결되어 있기 때문에 항상 root 노드부터 시작함 => 트리의 노드에 무작위로 access 할 수 없다는 뜻임
- 트리 순회에는 3가지 방법이 있음
- Preorder traversal
- Inorder traversal
- Postorder traversal
1.1 Preorder traversal
- root -> 왼쪽 하위 트리 -> 오른쪽 하위 트리
- 알고리즘
- 모든 노드를 통과할 때까지
- Step 1 : root 노드 방문
- Step 2 : 왼쪽 하위 트리를 재귀적으로 순회
- Step 3 : 오른쪽 하위 트리를 재귀적으로 순회
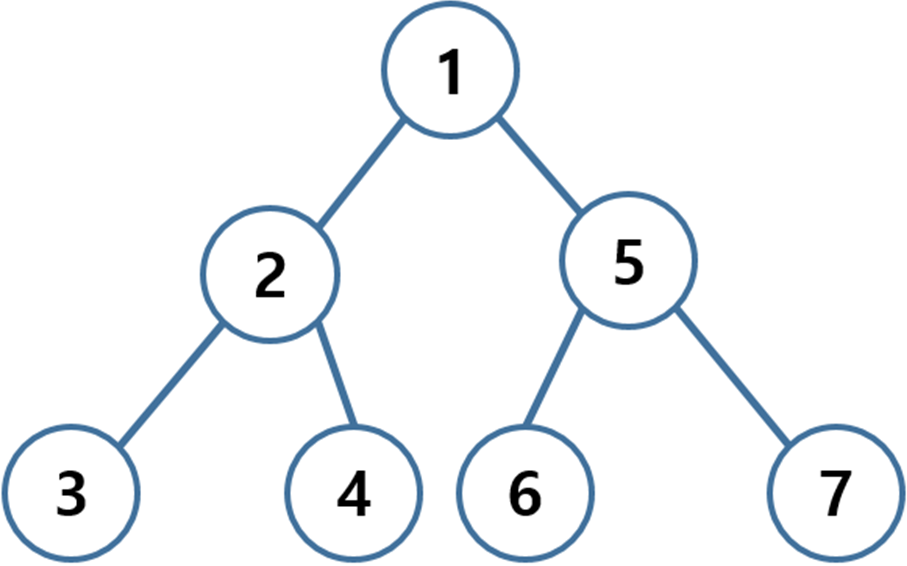
트리 그림 - 트리 그림에서 preorder traversal은 1, 2, 3, 4, 5, 6, 7 순서로 방문하게 됨
1.2 Inorder traversal
- 왼쪽 하위 트리 -> root -> 오른쪽 하위 트리
- Algorithm
- 모든 노드를 통과할 때까지
- Step 1 : 왼쪽 하위 트리를 재귀적으로 순회
- Step 2 : root 노드 방문
- Step 3 : 오른쪽 하위 트리를 재귀적으로 순회
- 트리 그림에서 inorder traversal은 3, 2, 4, 1, 5, 6, 7 순서로 방문하게 됨
1.3 Postorder traversal
- 왼쪽 하위 트리 -> 오른쪽 하위 트리 -> root
- Algorithm
- 모든 노드를 통과할 때까지
- Step 1 : 왼쪽 하위 트리를 재귀적으로 순회
- Step 2 : 오른쪽 하위 트리를 재귀적으로 순회
- Step 3 : root 노드 방문
- 트리 그림에서 inorder traversal은 3, 4, 2, 6, 7, 5, 1 순서로 방문하게 됨
2. Depth-First Search (DFS)
- DFS에서 가장 깊은 노드를 방문함
- 즉, 하나의 경로를 가능한 깊게 가고 막다른 골목에 다다르면 뒤로 물러서서 end에 도착할 때까지 다른 경로를 시도함
- DFS는 stack을 사용해 막다른 골목에 도달했을 때 어디로 가야할지 기억함
- DFS에서 트리의 모든 branch를 통과해야 하고 adjacent 노드를 통과해야 함
- 그래서 current 노드를 계속 추적하기 위해 stack으로 구현할 수 있는 last in first out(후입선출) 접근법이 필요함
- 노드의 depth에 도달하면 모든 노드가 stack에서 튀어나옴
- 그런 다음, 아직 방문하지 않은 adjacent 노드를 탐색함
- 만약 선입선출 방식인 queue로 구현된 경우 current 노드를 dequeue하기 전에 depth에 도달할 수 없음
- 아래의 예를 보자
- 먼저 stack과 방문한 노드를 기록하기 위한 visited를 초기화함
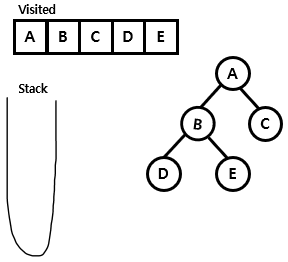
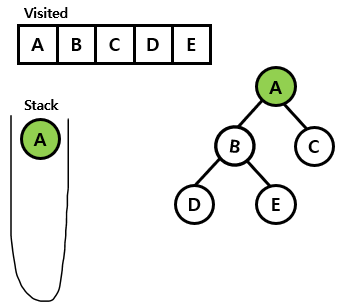
- A 노드를 stack에 push함
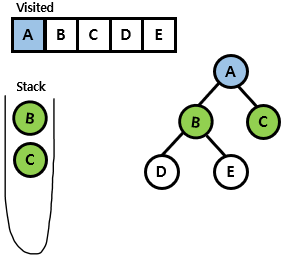
- A 노드를 visited 표시(blue)하고 A 노드의 방문하지 않은 adjacent 노드를 탐색함. 여기서는 B, C가 있으며 이를 stack에 push함
- stack의 가장 상단에 있는 B를 꺼내어 B 노드를 visited 표시하고 B 노드의 방문하지 않은 adjacent 노드를 탐색함. 여기서는 D, E가 있으며 이를 stack에 push함
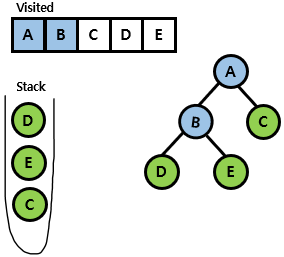
- D 노드를 visited 표시함. 여기서 D노드의 adjacent 노드 중에서 방문하지 않은 노드가 없기 때문에 stack에 push하는 과정은 패스하고 B 노드로 돌아감.
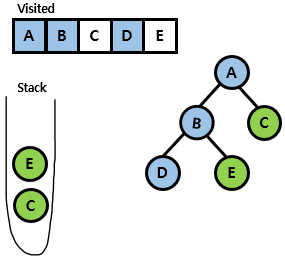
- E 노드를 visited 표시함. E 노드도 마찬가지로 방문하지 않은 adjacent 노드가 없기 때문에 pass.
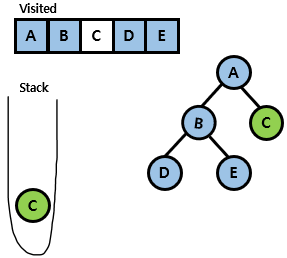
- C 노드를 visited 표시함. C 노드도 마찬가지로 모든 adjacent 노드들을 방문했으므로 pop하고 끝!
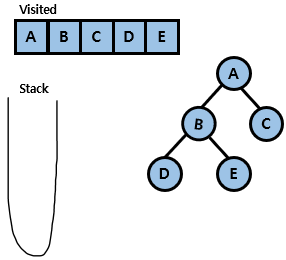
- 먼저 stack과 방문한 노드를 기록하기 위한 visited를 초기화함
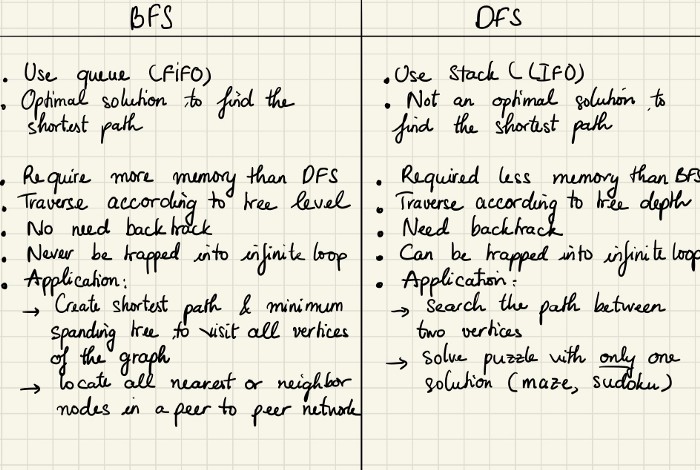
- 장점
- 이진 트리에서 DFS는 일반적으로 BFS보다 메모리를 덜 요구함
- DFS는 recursion(재귀)으로 쉽게 구현될 수 있음
- 단점
- DFS는 반드시 최단 경로를 찾지 않음. 반면 BFS는 검색함
- DFS in Python
- adjacency list와 starting node A가 주어지면 다음 recursive dfs 함수를 사용해 tree의 모든 노드를 찾을 수 있음
- dfs 함수는 다음 알고리즘을 따름
- 먼저, current node가 방문하지 않았는지 확인함 - 만약 방문하지 않았으면 visited set에 추가함
- 그런 다음, current node의 각 neighbor에 대해 dfs 함수가 다시 호출됨
- 모든 노드를 방문할 때 이 base case가 호출됨. 그런 다음 함수가 반환됨
- 코드는 다음과 같음
출력 결과는 아래와 같음# tree를 표현하기 위해 adjacency list를 사용하고 python dictionary로 구현함 graph = { 'A': ['B', 'C'], 'B': ['D', 'E'], 'C': [], 'D': [], 'E': [] } # visited node를 기록하기 위해 visited를 다음과 같이 정의함 visited = set() def dfs(graph, visited, node): # 먼저, current node가 방문하지 않았는지 확인함 if node not in visited: print(node) visited.add(node) # 만약 방문하지 않았으면 visited set에 추가함 # 그런 다음, current node의 각 neighbor에 대해 for neighbor in graph[node]: dfs(graph, visited, neighbor) # dfs 함수가 다시 호출됨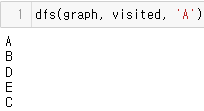
3. Breadth-First Search (BFS)
- BFS에서 wide net을 캐스팅(casting)하여 tree의 모든 노드를 검색함
- 즉, 먼저 전체 수준(level)의 children 노드를 통과한 후 grandchilren 노드를 통과함
- BFS는 먼저 가장 가까운 노드들을 먼저 탐색한 다음 source(가장 가까운 노드들)에서 outwards(다음 level의 노드들)로 이동함
- 이를 생각해, 쿼리할 때 삽입된 순서에 따라 가장 오래된(먼저 들어간) element를 제공하는 data structure를 사용하고자 함
- 이 경우 queue가 first in first out(FIFO)이기에 적합함
- 아래의 예를 보자
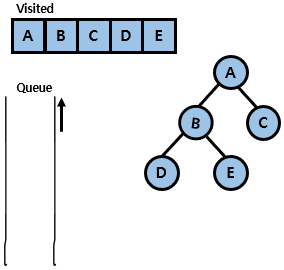
- 먼저 queue와 방문한 노드를 기록하기 위한 visited를 초기화함
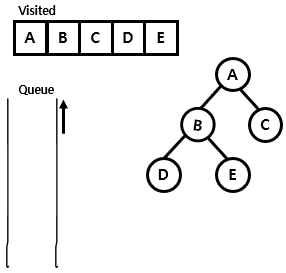
- root 노드인 A 노드부터 시작함. queue에 A 노드를 enqueue 함
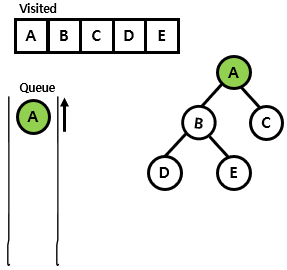
- A 노드를 visited 표시(blue)하고 A 노드의 방문하지 않은 adjacent 노드를 탐색함. 여기서는 B, C가 있으며 이를 queue에 enqueue함
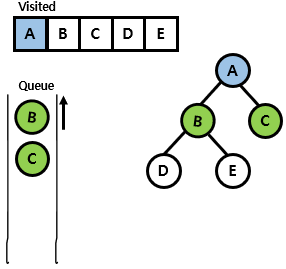
- B 노드를 visited 표시하고 B 노드의 방문하지 않은 adjacent 노드를 탐색함. 여기서는 D, E가 있으며 이를 queue에 enqueue함
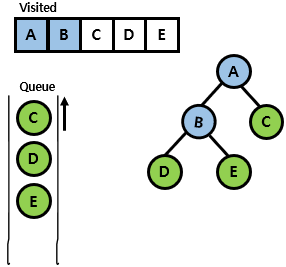
- C 노드를 visited 표시함. 여기서 C 노드의 adjacent 노드 중에서 방문하지 않은 노드가 없으므로 queue에 enqueue하는 과정은 pass
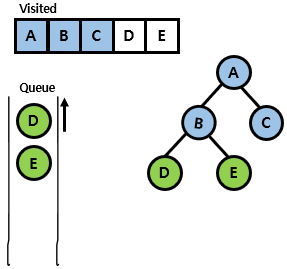
- D 노드를 visited 표시하고 queue에서 dequeue함
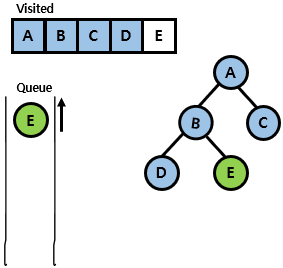
- E 노드를 visited 표시하고 방문하지 않은 모든 노드를 얻기 위해 dequeuing을 계속하고 queue가 비워지면 program은 끝
- 먼저 queue와 방문한 노드를 기록하기 위한 visited를 초기화함
- 장점
- BFS는 구현하기 쉬움
- BFS는 모든 탐색 문제에 적용될 수 있음
- BFS는 DFS에 비해 잠재적인 무한 루프 문제를 겪지 않음. 무한 루프 문제로 인해 컴퓨터가 충돌할 수 있지만 DFS는 심증 탐색을 수행함
- BFS는 links의 가중치가 균일한 경우 항상 최단 경로를 찾음. 그래서 BFS는 완전하고 최적임
- 단점
- 논의한 바와 같이, BFS에서 메모리 사용률이 좋지 않으므로 BFS가 DFS 보다 더 많은 메모리가 필요하다고 말 할 수 있음
- BFS는 ' blind' 탐색임. 즉, 탐색 공간이 엄청남. 탐색 성능은 다른 heuristic 탐색에 비해 약함
- BFS in Python
- bfs 함수는 다음 알고리즘을 따름
- 먼저, 시작 노드를 확인하고 시작 노드를 visited list와 queue에 추가함
- 그런 다음, queue에 elements가 포함되어 있는 동안, queue에서 노드를 계속 제거하고 해당 노드의 neighbors가 방문하지 않은 경우 queue에 추가하고 방문한 것으로 표시함
- queue가 비워질 때까지 계속 함
- 코드는 다음과 같음
# tree를 표현하기 위해 adjacency list를 사용하고 python dictionary로 구현함 graph = { 'A': ['B', 'C'], 'B': ['D', 'E'], 'C': [], 'D': [], 'E': [] } # visited node를 기록하기 위해 visited를 다음과 같이 정의함 visited = [] # 현재 queue에 있는 노드를 추적하기 위해 다음과 같이 정의함 queue = [] def bfs(visited, graph, node): # 먼저, 시작 노드를 확인하고 visited.append(node) # 시작 노드를 visited list에 추가 queue.append(node) # 시작 노드를 queue에 추가 # queue에 elements가 포함되어 있는 동안 진행 while queue: s=queue.pop(0) # queue에서 노드를 계속 제거 print(s, end=" ") # 해당 노드의 neighbors에 접근 for neighbor in graph[s]: # 해당 노드의 neighbors가 방문하지 않은 경우 if neighbor not in visited: visited.append(neighbor) # 해당 노드 visited에 추가 queue.append(neighbor) # 해당 노드 queue에 추가
출력 결과는 다음과 같음
- bfs 함수는 다음 알고리즘을 따름
4. BFS vs DFS
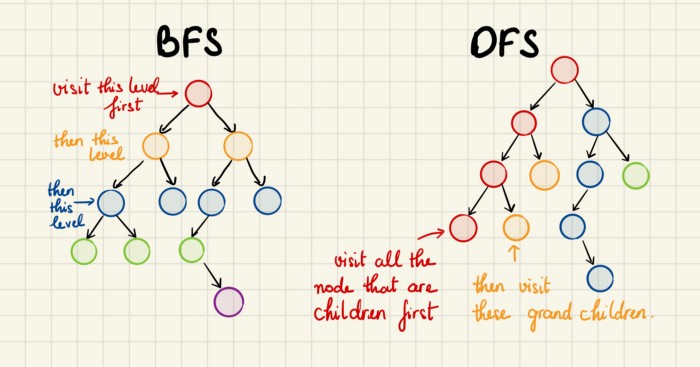
https://medium.com/nothingaholic/depth-first-search-vs-breadth-first-search-in-python-81521caa8f44 - 언저 BFS 혹은 DFS를 사용해야 할까?
- solution이 트리의 root와 멀지 않은 경우 BFS가 더 나을 수 있음
- 트리가 매우 깊고 solutions이 rare한 경우 DFS는 오랜 시간이 걸릴 수 있지만 BFS는 더 빠를 수 있음
- 트리가 넓은(wide) 경우 BFS는 많은 메모리를 필요로 하여 비실용적일 수 있음
- solutions가 frequent 하지만 트리 깊숙한 곳에 있는 경우 BFS가 비실용적일 수 있음
- 일반적으로 다음과 같음
- BFS - 특정 source node에서 특정 목적지까지의 최단 경로를 찾고 싶을 때 (일반적으로, 주어진 초기 state에서 end state까지 도달하는 최소한의 steps)
- DFS - 모든 가능성 있는 경우를 탐색하고 어떤 것이 best인지 확인하고 싶을 때
- BFS or DFS - 주어진 graph에서 두 노드 간의 연결성을 확인하려는 경우 (일반적으로, 주어진 state에서 다른 state로 도달할 수 있는지 여부, whether we could reach a given state to another)
https://medium.com/nothingaholic/depth-first-search-vs-breadth-first-search-in-python-81521caa8f44 728x90반응형'Data Structure' 카테고리의 다른 글
Python으로 구현하는 Linked List (3) 양방향 Linked List (0) 2022.09.07 Python으로 구현하는 Linked List (2) 단방향 Linked List (0) 2022.09.06 Python으로 구현하는 Linked List (1) 간단한 단방향 Linked List (0) 2022.08.31 Python으로 Linked List 간단히 구현하기 (0) 2022.08.29 기초 자료 구조 (0) 2022.02.06